小波以游戏方式决定：是去打球、唱歌还是去下棋.游戏规则为：以O为起点,再从A1,A2,A3,A4,A5,A6(如图)这6个点中任取两点分别为终点得到两个向量，记这两个向量的数量积为X,若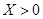
就去打球；若
就去唱歌；若
就去下棋.
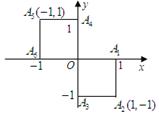
（Ⅰ）写出数量积X的所有可能取值;
（Ⅱ）分别求小波去下棋的概率和不去唱歌的概率.
相关试题
．
的解集；
，若存在
,使
，求
的取值范围。
，关于
的不等式
在
上恒成立，求实数
的取值范围．
的单调区间;
>0,求
上的最大值．
为奇函数。
的值；
在区间（1，
）上是减函数；
．
，
，求实数
的值；
，求实数
，
，
；（2）
；（3）
推荐套卷
小波以游戏方式决定：是去打球、唱歌还是去下棋.游戏规则为：以O为起点,再从A1,A2,A3,A4,A5,A6(如图)这6个点中任取两点分别为终点得到两个向量，记这两个向量的数量积为X,若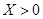就去打球；若就去唱歌；若就去下棋.
（Ⅰ）写出数量积X的所有可能取值;
（Ⅱ）分别求小波去下棋的概率和不去唱歌的概率.
粤公网安备 44130202000953号