如图，在正方形ABCD中，点P是AB的中点，连接DP，过点B作BE⊥DP交DP的延长线于点E，连接AE，过点A作AF⊥AE交DP于点F，连接BF．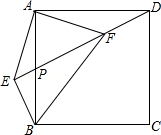
（1）若AE=2，求EF的长；
（2）求证：PF=EP+EB．
相关试题
.
相关知识点
推荐套卷
如图，在正方形ABCD中，点P是AB的中点，连接DP，过点B作BE⊥DP交DP的延长线于点E，连接AE，过点A作AF⊥AE交DP于点F，连接BF．
（1）若AE=2，求EF的长；
（2）求证：PF=EP+EB．
粤公网安备 44130202000953号