已知：如图，点C为线段AB上一点，△ACM、△CBN是等边三角形，可以说明：△ACN≌△MCB，从而得到结论：AN=BM．现要求：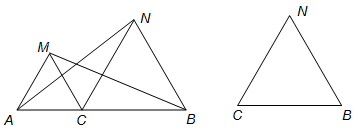
（1）将△ACM绕C点按逆时针方向旋转180°，使A点落在CB上．请对照原题图在下图中画出符合要求的图形（不写作法，保留作图痕迹）．
（2）在（1）所得到的图形中，结论“AN=BM”是否还成立？若成立，请给予证明；若不成立，请说明理由．
（3）在（1）所得到的图形中，设MA的延长线与BN相交于D点，请你判断△ABD与四边形MDNC的形状，并说明你的结论的正确性．
相关试题
如图是两个全等的含30°角的直角三角形．
（1）将其相等边拼在一起，组成一个没有重叠部分的平面图形，请你画出所有不同的拼接平面图形的示意图；
（2）若将（1）中平面图形分别印制在质地、形状、大小完全相同的卡片上，洗匀后从中随机抽取一张，求抽取的卡片上平面图形为轴对称图形的概率．
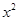+2x+2k－2=0有两个不相等的实数根．
，其中x是－3＜x＜2的整数解．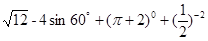
；
．
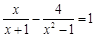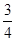x+3与y轴交于点C，，与x轴交于点D．点P是x轴上方的抛物线上一动点，过点P作PF⊥x轴于点F，交直线CD于点E．设点P的横坐标为m。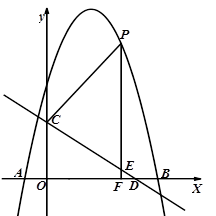
相关知识点
推荐套卷
粤公网安备 44130202000953号