国家推行“节能减排，低碳经济”的政策后，某企业推出一种叫“CNG”的改烧汽油为天然气的装置，每辆车改装费为b元.据市场调查知：每辆车改装前、后的燃料费（含改装费）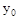
、
（单位：元）与正常运营时间
（单位：天）之间分别满足关系式：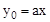
、
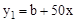，如图所示.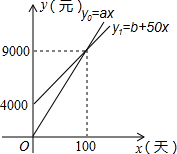
试根据图像解决下列问题：
（1）每辆车改装前每天的燃料费
= 元,每辆车的改装费b= 元.正常运营 天后，就可以从节省燃料费中收回改装成本.
（2）某出租汽车公司一次性改装了100辆车，因而，正常运营多少天后共节省燃料费40万元？
相关试题
……将你猜想到的规律用n的一个等式来表示：.
，
、
分别是
、
的中点，
分别交
、
于点
、
.你能说出
与
的大小关系并加以证明吗?
三角形中位线定理，是我们非常熟悉的定理.
①请你在下面的横线上，完整地叙述出这理:____________________________________.
②根据这个定理画出图形，写出已知和求证，并对该定理给出证明.
相关知识点
推荐套卷
粤公网安备 44130202000953号