已知椭圆C：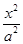
＋
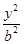＝1(a＞b＞0)的离心率e＝
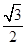，椭圆C的上、下顶点分别为A1，A2，左、右顶点分别为B1，B2,左、右焦点分别为F1，F2．原点到直线A2B2的距离为
．
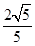（1）求椭圆C的方程；
（2）过原点且斜率为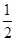
的直线l，与椭圆交于E，F点，试判断∠EF2F是锐角、直角还是钝角，并写出理由；
（3）P是椭圆上异于A1，A2的任一点,直线PA1，PA2，分别交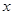
轴于点N，M,若直线OT与过点M，N 的圆G相切，切点为T.证明：线段OT的长为定值,并求出该定值.
若
则方程
无实数根。
的一元二次不等式
对于一切实数
，求证：
不可能都是奇数。
，写出“
”形式的命题，并判断“
（其中全集
，
，
）. 
推荐套卷
已知椭圆C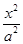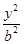：＋＝1(a＞b＞0)的离心率e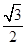＝，椭圆C的上、下顶点分别为A1，A2，左、右顶点分别为B1，B2,左、右焦点分别为F1，F2．原点到直线A2B2的距离为．
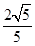（1）求椭圆C的方程；
（2）过原点且斜率为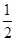的直线l，与椭圆交于E，F点，试判断∠EF2F是锐角、直角还是钝角，并写出理由；
（3）P是椭圆上异于A1，A2的任一点,直线PA1，PA2，分别交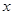轴于点N，M,若直线OT与过点M，N 的圆G相切，切点为T.证明：线段OT的长为定值,并求出该定值.
粤公网安备 44130202000953号