某社区举办防控甲型H7N9流感知识有奖问答比赛，甲、乙、丙三人同时回答一道卫生知识题，三人回答正确与错误互不影响。已知甲回答这题正确的概率是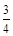
，甲、丙两人都回答错误的概率是
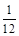，乙、丙两人都回答正确的概率是
.
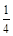(I)求乙、丙两人各自回答这道题正确的概率；
(II)用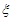
表示回答该题正确的人数，求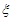的分布列和数学期望
.
相关试题
中，底面是矩形
，其中
，
，侧面
是等边三角形，且与底面
为
的中点．
面
；
的余弦值．
满足
，
（
）．
是等差数列；
，数列
的前
项和
，求数列
的前
．
、
是直线
与函数
（
）图象的相邻两个交点，且
．
的值；
的内角
的对边分别为
，
，求
的取值范围．
，
，
为自然对数的底数.
时，求函数
在点
处的切线方程；
，比较
与
的大小，并加以证明.
（
）的离心率
.点
分别为椭圆
的左焦点和右顶点，且
.
作一条直线
交椭圆
两点，点
关于
轴的对称点为
.若
，求证：
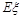.推荐套卷
某社区举办防控甲型H7N9流感知识有奖问答比赛，甲、乙、丙三人同时回答一道卫生知识题，三人回答正确与错误互不影响。已知甲回答这题正确的概率是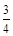，甲、丙两人都回答错误的概率是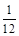，乙、丙两人都回答正确的概率是.
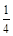(I)求乙、丙两人各自回答这道题正确的概率；
(II)用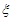表示回答该题正确的人数，求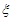的分布列和数学期望.
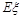粤公网安备 44130202000953号