扬州某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边成角为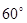 (如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为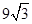 平方米,且高度不低于
平方米,且高度不低于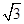 米.记防洪堤横断面的腰长为
米.记防洪堤横断面的腰长为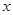 (米),外周长(梯形的上底线段
(米),外周长(梯形的上底线段 与两腰长的和)为
与两腰长的和)为 (米).
(米).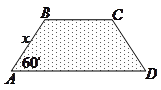
⑴求 关于
关于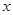 的函数关系式,并指出其定义域;
的函数关系式,并指出其定义域;
⑵要使防洪堤横断面的外周长不超过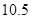 米,则其腰长
米,则其腰长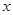 应在什么范围内?
应在什么范围内?
⑶当防洪堤的腰长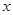 为多少米时,堤的上面与两侧面的水泥用料最省(即断面的外周长最小)?求此时外周长的值.
为多少米时,堤的上面与两侧面的水泥用料最省(即断面的外周长最小)?求此时外周长的值.
相关知识点
推荐套卷
 是否存在实数根.
是否存在实数根. 的反函数为
的反函数为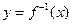 ,定义:若对给定的实数
,定义:若对给定的实数 ,函数
,函数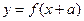 与
与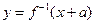 互为反函数,则称
互为反函数,则称 是否满足“1和性质”,并说明理由;(2)若
是否满足“1和性质”,并说明理由;(2)若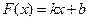 ,其中
,其中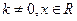 满足“2和性质”,则是否存在实数a,使得
满足“2和性质”,则是否存在实数a,使得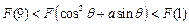 对任意的
对任意的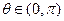 恒成立?若存在,求出的范围;若不存在,请说明理由.
恒成立?若存在,求出的范围;若不存在,请说明理由.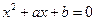 有两个根,一个根在区间
有两个根,一个根在区间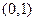 内,另一根在区间
内,另一根在区间 内,记点
内,记点 对应的区域为
对应的区域为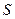 .(1)设
.(1)设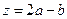 ,求的取值范围;(2)过点
,求的取值范围;(2)过点 的一束光线,射到轴被反射后经过区域
的一束光线,射到轴被反射后经过区域 经过区域
经过区域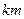 的圆形村落,A、B两人同时从村落中心出发,B向北直行,A先向东直行,出村后不久,改变前进方向,沿着与村落周界相切的直线前进,后来恰与B相遇.设A、B两人速度一定,其速度比为3:1,问两人在何处相遇?
的圆形村落,A、B两人同时从村落中心出发,B向北直行,A先向东直行,出村后不久,改变前进方向,沿着与村落周界相切的直线前进,后来恰与B相遇.设A、B两人速度一定,其速度比为3:1,问两人在何处相遇?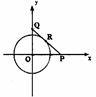
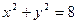 内有一点
内有一点 ,
, 为过点
为过点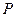 且倾斜角为
且倾斜角为 的弦,
的弦,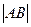 ;
;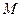 ,求点
,求点
 粤公网安备 44130202000953号
粤公网安备 44130202000953号