一个袋中装有大小相同的球10个，其中红球8个，黑球2个，现从袋中有放回地取球，每次随机取1个． 求：
（Ⅰ）连续取两次都是红球的概率；
（Ⅱ）如果取出黑球，则取球终止，否则继续取球，直到取出黑球，取球次数最多不超过4次，求取球次数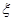
的概率分布列及期望．
相关试题
(2)
。
的零点；
），则该几何体的体积。
推荐套卷
一个袋中装有大小相同的球10个，其中红球8个，黑球2个，现从袋中有放回地取球，每次随机取1个． 求：
（Ⅰ）连续取两次都是红球的概率；
（Ⅱ）如果取出黑球，则取球终止，否则继续取球，直到取出黑球，取球次数最多不超过4次，求取球次数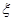的概率分布列及期望．
粤公网安备 44130202000953号