如图，边长为a的等边三角形ABC的中线AF与中位线DE交于点G，将△ADE绕DE旋转得到△A′DE（A′
平面ABC），则下列叙述错误的是（ ）
A. 平面A′FG⊥平面ABC
B. BC∥平面A′DE
C. 三棱锥A′-DEF的体积最大值为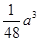
D. 直线DF与直线A′E不可能共面
)4的值是
的值是
i
+
i,则1+ω等于
=a+3i,则a等于
+
i,A={x|x=ωk+ω－k,k∈Z},则集合A中的元素有推荐套卷
如图，边长为a的等边三角形ABC的中线AF与中位线DE交于点G，将△ADE绕DE旋转得到△A′DE（A′ 平面ABC），则下列叙述错误的是（ ）
A. 平面A′FG⊥平面ABC
B. BC∥平面A′DE
C. 三棱锥A′-DEF的体积最大值为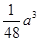
D. 直线DF与直线A′E不可能共面
粤公网安备 44130202000953号