设点A（
，0），B（
，0），直线AM、BM相交于点M，且它们的斜率之积为
.
（Ⅰ）求动点M的轨迹C的方程；
（Ⅱ）若直线
过点F（1，0）且绕F旋转，与圆
相交于P、Q两点，与轨迹C相交于R、S两点，若|PQ|
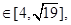求△
的面积的最大值和最小值（F′为轨迹C的左焦点）.
，
．
的值；
，求
．
为异面直线
的公垂线，
平面
，
平面
，
．求证：
．
环、9环、8环、7环的概率分别为
，
，
，
，计算该射手在一次射击中：
环的概率；推荐套卷
设点A（，0），B（，0），直线AM、BM相交于点M，且它们的斜率之积为.
（Ⅰ）求动点M的轨迹C的方程；
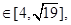（Ⅱ）若直线过点F（1，0）且绕F旋转，与圆相交于P、Q两点，与轨迹C相交于R、S两点，若|PQ|求△的面积的最大值和最小值（F′为轨迹C的左焦点）.
粤公网安备 44130202000953号