某社区有甲、乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同.甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.小张准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于15小时,也不超过40小时.
(1)设在甲家租一张球台开展活动 小时的收费为
小时的收费为 元
元 ,在乙家租一张球台开展活动
,在乙家租一张球台开展活动 小时的收费为
小时的收费为 元
元 .试求
.试求 和
和 .
.
(2)问:小张选择哪家比较合算?为什么?
相关知识点
推荐套卷
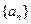 的前
的前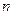 项和为
项和为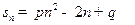 (
( )
)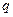 的值;
的值;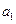 与
与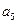 的等差中项为18,
的等差中项为18,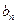 满足
满足 ,求数列
,求数列 的前
的前
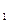 B
B


 的不等式
的不等式 ,
, 恒成立;
恒成立; 是增函数,
是增函数, 是真命题,求实数
是真命题,求实数 的取值范围.
的取值范围.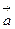 =(1,
=(1,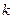 ),
),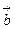 =(2
=(2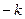 ),(
),(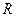 ).
).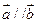 ,求
,求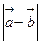 的值;
的值;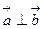 ,求
,求
 .
.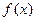 的最大值与最小正周期;
的最大值与最小正周期; 粤公网安备 44130202000953号
粤公网安备 44130202000953号