本学期开学初，学校体育组对九年级某班50名学生进行了跳绳项目的测试，根据测试成绩制作了下面两个统计图。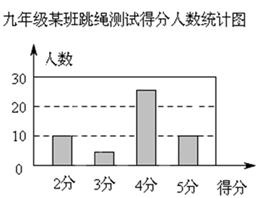
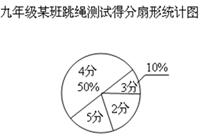
根据统计图解答下列问题：
（1）本次测试的学生中，得4分的学生有多少人？
（2）本次测试的平均分是多少分？
（3）通过一段时间的训练，体育组对该班学生的跳绳项目进行了第二次测试，测得成绩的最低分为3分。且得4分和5分的人数共有45人，平均分比第一次提高了0.8分，问第二次测试中得4分、5分的学生各有多少人？
相关试题
如图，点A在∠O的一边OA上．按要求画图并填空：
（1）过点A画直线AB ⊥OA，与∠O的另一边相交于点B；
（2）过点A画OB的垂线段AC，垂足为点C；
（3）过点C画直线CD∥OA ，交直线AB于点D；
（4）∠CDB=°；
（5）如果OA=8，AB=6，OB=10，则点A到直线OB的距离为．
某地为更好治理湖水水质，治污部门决定购买10台污水处理设备．现有
两种型号的设备，其中每台的价格，月处理污水量如下表：
 型 |
 型 |
|
| 价格（万元/台） |
 |
 |
| 处理污水量（吨/月） |
240 |
200 |
经调查：购买一台型设备比购买一台型设备多2万元，购买2台型设备比购买3台型设备少6万元．
（1）求
的值．
（2）经预算：治污部门购买污水处理设备的资金不超过105万元，你认为该部门有哪几种购买方案．
（3）在（2）问的条件下，若每月要求处理的污水量不低于2040吨，为了节约资金，请你为治污部门设计一种最省钱的购买方案．
，
，点
在
轴上，
．
，求点
的坐标．
，并写出该不等式组的整数解．
，并把解集在数轴上表示出来．相关知识点
推荐套卷
粤公网安备 44130202000953号