在平面直角坐标系xOy中，直线y=kx（k为常数）与抛物线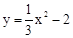
交于A，B两点，且A点在y轴左侧，P点的坐标为（0，﹣4），连接PA，PB．有以下说法：
①PO2=PA•PB；
②当k＞0时，（PA+AO）（PB﹣BO）的值随k的增大而增大；
③当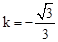
时，BP2=BO•BA；
④△PAB面积的最小值为
．
其中正确的是 （写出所有正确说法的序号）
，求
=.
；（2）
.
相关知识点
推荐套卷
在平面直角坐标系xOy中，直线y=kx（k为常数）与抛物线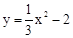交于A，B两点，且A点在y轴左侧，P点的坐标为（0，﹣4），连接PA，PB．有以下说法：
①PO2=PA•PB；
②当k＞0时，（PA+AO）（PB﹣BO）的值随k的增大而增大；
③当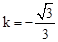时，BP2=BO•BA；
④△PAB面积的最小值为．
其中正确的是 （写出所有正确说法的序号）
粤公网安备 44130202000953号