如图1,一辆汽车的背面,有一种特殊形状的刮雨器,忽略刮雨器的宽度可抽象为一条折线OAB,如图2所示,量得连杆OA长为10cm,雨刮杆AB长为48cm,∠OAB=1200.若启动一次刮雨器,雨刮杆AB正好扫到水平线CD的位置,如图3所示.
(1)求雨刮杆AB旋转的最大角度及O、B两点之间的距离;(结果精确到0.01)
(2)求雨刮杆AB扫过的最大面积.(结果保留π的整数倍)
(参考数据:sin60°=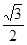 ,cos60°=
,cos60°=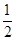 ,tan60°=
,tan60°=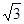 ,
,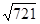 ≈26.851,可使用科学计算器)
≈26.851,可使用科学计算器)
推荐套卷
如图1,一辆汽车的背面,有一种特殊形状的刮雨器,忽略刮雨器的宽度可抽象为一条折线OAB,如图2所示,量得连杆OA长为10cm,雨刮杆AB长为48cm,∠OAB=1200.若启动一次刮雨器,雨刮杆AB正好扫到水平线CD的位置,如图3所示.
(1)求雨刮杆AB旋转的最大角度及O、B两点之间的距离;(结果精确到0.01)
(2)求雨刮杆AB扫过的最大面积.(结果保留π的整数倍)
(参考数据:sin60°=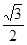 ,cos60°=
,cos60°=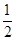 ,tan60°=
,tan60°=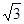 ,
,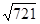 ≈26.851,可使用科学计算器)
≈26.851,可使用科学计算器)