如图,一只猫头鹰蹲在一棵树AC的B(点B在AC上)处,发现一只老鼠躲进短墙DF的另一侧,猫头鹰的视线被短墙遮住,为了寻找这只老鼠,它又飞至树顶C处,已知短墙高DF=4米,短墙底部D与树的底部A的距离为2.7米,猫头鹰从C点观测F点的俯角为53°,老鼠躲藏处M(点M在DE上)距D点3米.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)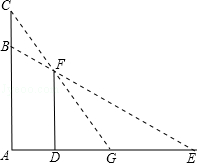
(1)猫头鹰飞至C处后,能否看到这只老鼠?为什么?
(2)要捕捉到这只老鼠,猫头鹰至少要飞多少米(精确到0.1米)?
相关知识点
推荐套卷
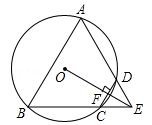

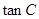 。
。 的正方形AEFG按图1位置放置,AD与AE在同一条直线上,AB与AG在同一条直线上.
的正方形AEFG按图1位置放置,AD与AE在同一条直线上,AB与AG在同一条直线上.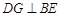 ,请你帮他说明理由.
,请你帮他说明理由.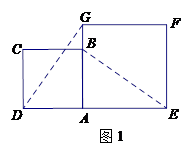

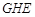 与△
与△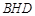 面积之和的最大值,并简要说明理由.
面积之和的最大值,并简要说明理由.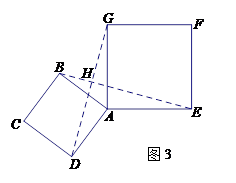

 ;
; ,EF=
,EF= ,∠BAD=60°,且AB
,∠BAD=60°,且AB .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号