已知平面直角坐标系xOy(如图),直线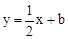 经过第一、二、三象限,与y轴交于点B,点A(2,t)在这条直线上,连接AO,△AOB的面积等于1.
经过第一、二、三象限,与y轴交于点B,点A(2,t)在这条直线上,连接AO,△AOB的面积等于1.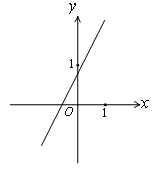
(1)求b的值;
(2)如果反比例函数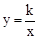 (
(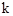 是常量,
是常量,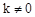 )的图像经过点A,求这个反比例函数的解析式.
)的图像经过点A,求这个反比例函数的解析式.
相关知识点
推荐套卷
已知平面直角坐标系xOy(如图),直线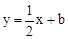 经过第一、二、三象限,与y轴交于点B,点A(2,t)在这条直线上,连接AO,△AOB的面积等于1.
经过第一、二、三象限,与y轴交于点B,点A(2,t)在这条直线上,连接AO,△AOB的面积等于1.
(1)求b的值;
(2)如果反比例函数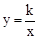 (
(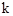 是常量,
是常量,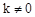 )的图像经过点A,求这个反比例函数的解析式.
)的图像经过点A,求这个反比例函数的解析式.