已知椭圆 的长轴两端点分别为
的长轴两端点分别为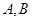 ,
, 是椭圆上的动点,以
是椭圆上的动点,以 为一边在
为一边在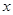 轴下方作矩形
轴下方作矩形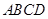 ,使
,使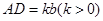 ,
,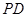 交
交 于点
于点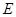 ,
,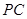 交
交 于点
于点 .
.
(Ⅰ)如图(1),若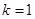 ,且
,且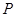 为椭圆上顶点时,
为椭圆上顶点时, 的面积为12,点
的面积为12,点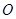 到直线
到直线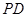 的距离为
的距离为 ,求椭圆的方程;
,求椭圆的方程;
(Ⅱ)如图(2),若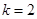 ,试证明:
,试证明: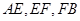 成等比数列.
成等比数列.
推荐套卷
已知椭圆 的长轴两端点分别为
的长轴两端点分别为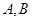 ,
, 是椭圆上的动点,以
是椭圆上的动点,以 为一边在
为一边在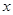 轴下方作矩形
轴下方作矩形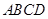 ,使
,使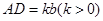 ,
,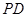 交
交 于点
于点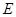 ,
,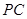 交
交 于点
于点 .
.
(Ⅰ)如图(1),若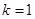 ,且
,且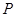 为椭圆上顶点时,
为椭圆上顶点时, 的面积为12,点
的面积为12,点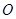 到直线
到直线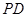 的距离为
的距离为 ,求椭圆的方程;
,求椭圆的方程;
(Ⅱ)如图(2),若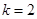 ,试证明:
,试证明: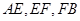 成等比数列.
成等比数列.