如图,在边长为1小正方形组成的10×10网格中(我们把组成网格的小正方形的顶点称为格点),四边形ABCD在直线l的左侧,其四个顶点A、B、C、D分别在网格的格点上。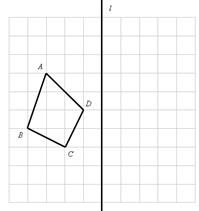
(1)请你在所给的网格中画出四边形 ,使四边形
,使四边形 和四边形ABCD关于直线l对称,
和四边形ABCD关于直线l对称,
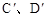 分别是点A、B、C、D的对称点;
分别是点A、B、C、D的对称点;
(2)在(1)的条件下,结合你画的图形,直接写出线段 的长度。
的长度。
相关知识点
推荐套卷
如图,在边长为1小正方形组成的10×10网格中(我们把组成网格的小正方形的顶点称为格点),四边形ABCD在直线l的左侧,其四个顶点A、B、C、D分别在网格的格点上。
(1)请你在所给的网格中画出四边形 ,使四边形
,使四边形 和四边形ABCD关于直线l对称,
和四边形ABCD关于直线l对称,
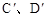 分别是点A、B、C、D的对称点;
分别是点A、B、C、D的对称点;
(2)在(1)的条件下,结合你画的图形,直接写出线段 的长度。
的长度。