甲、乙两人在玩转盘游戏时，把两个可以自由转动的转盘A、B分成4等份、3等份的扇形区域，并在每一小区域内标上数字（如图所示），指针的位置固定．游戏规则：同时转动两个转盘，当转盘停止后，若指针所指两个区域的数字之和为3的倍数，甲胜；若指针所指两个区域的数字之和为4的倍数时，乙胜．如果指针落在分割线上，则需要重新转动转盘．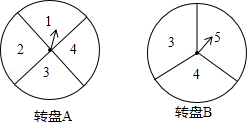
（1）试用列表或画树形图的方法，求甲获胜的概率；
（2）请问这个游戏规则对甲、乙双方公平吗？试说明理由．
相关试题
先阅读理解下面的例题，再按要求解答下列问题：
例题：求代数式
的最小值.
解：
的最小值是
.
（1）求代数式
的最小值；
（2）求代数式
的最大值；
（3）某居民小区要在一块一边靠墙（墙长
m）的空地上建一个长方形花园
，花园一边靠墙，另三边用总长为
m的栅栏围成. 如图，设
（m），请问:当
取何值时，花园的面积最大？最大面积是多少？
如图，长方形
中，
cm，
cm，现有一动点
从
出发以2cm/秒的速度，沿矩形的边
回到点，设点运动的时间为
秒.
（1）当
秒时，求
的面积；
（2）当为何值时，点与点的距离为5cm？
（3）当为何值时
，以线段
、
、
的长度为三边长的三角形是直角三角形，且是斜边.
的三边长分别为
,
,
.若将
折叠，点
正好落在
边上的点
处.求线段
的长度.
中，
，
cm，正方形
的面积为
cm2，
于点
，求
的长.
，其中
，
.相关知识点
推荐套卷
粤公网安备 44130202000953号