如图，已知抛物线y=ax2+bx﹣4经过A（﹣8，0），B（2，0）两点，直线x=﹣4交x轴于点C，交抛物线于点D．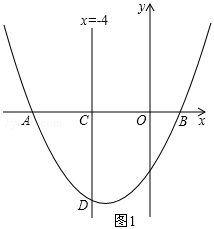
（1）求该抛物线的解析式；
（2）点P在抛物线上，点E在直线x=﹣4上，若以A，O，E，P为顶点的四边形是平行四边形，求点P的坐标；
（3）若B，D，C三点到同一条直线的距离分别是d1，d2，d3，问是否存在直线l，使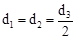
？若存在，请直接写出d3的值；若不存在，请说明理由．
，求
、
与
．
的位似图形A1B1C1D1，且四边形A1B1C1D1在第一象限。写出各点坐标。
其中
，
相关知识点
推荐套卷
如图，已知抛物线y=ax2+bx﹣4经过A（﹣8，0），B（2，0）两点，直线x=﹣4交x轴于点C，交抛物线于点D．
（1）求该抛物线的解析式；
（2）点P在抛物线上，点E在直线x=﹣4上，若以A，O，E，P为顶点的四边形是平行四边形，求点P的坐标；
（3）若B，D，C三点到同一条直线的距离分别是d1，d2，d3，问是否存在直线l，使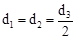？若存在，请直接写出d3的值；若不存在，请说明理由．
粤公网安备 44130202000953号