为了响应国家节能减排的号召,鼓励市民节约用电,我市从2012年7月1日起,居民用电实行“一户一表”的“阶梯电价”,分三个档次收费,第一档是用电量不超过180千瓦时实行“基本电价”,第二、三档实行“提高电价”,具体收费情况如右折线图,请根据图象回答下列问题;
(1)当用电量是180千瓦时时,电费是 元;
(2)第二档的用电量范围是 ;
(3)“基本电价”是 元/千瓦时;
(4)小明家8月份的电费是328.5元,这个月他家用电多少千瓦时?
相关知识点
推荐套卷
 ,求原铁皮的长
,求原铁皮的长
 的一元二次方程
的一元二次方程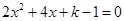 有实数根,
有实数根, 为正整数.
为正整数.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号