如图,抛物线y=ax2+bx+c的开口向下,与x轴交于点A(﹣3,0)和点B(1,0).与y轴交于点C,顶点为D.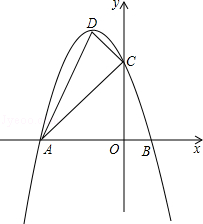
(1)求顶点D的坐标.(用含a的代数式表示);
(2)若△ACD的面积为3.
①求抛物线的解析式;
②将抛物线向右平移,使得平移后的抛物线与原抛物线交于点P,且∠PAB=∠DAC,求平移后抛物线的解析式.
相关知识点
推荐套卷
如图,抛物线y=ax2+bx+c的开口向下,与x轴交于点A(﹣3,0)和点B(1,0).与y轴交于点C,顶点为D.
(1)求顶点D的坐标.(用含a的代数式表示);
(2)若△ACD的面积为3.
①求抛物线的解析式;
②将抛物线向右平移,使得平移后的抛物线与原抛物线交于点P,且∠PAB=∠DAC,求平移后抛物线的解析式.