如图,在△ABC中,以AB为直径的⊙O交AC于点D,直径AB左侧的半圆上有一点动点E(不与点A、B重合),连结EB、ED。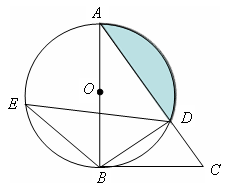
(1)如果∠CBD=∠E,求证:BC是⊙O的切线;
(2)当点E运动到什么位置时,△EDB≌△ABD,并给予证明;
(3)若tanE=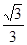 ,BC=
,BC=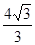 ,求阴影部分的面积。(计算结果精确到0.1)
,求阴影部分的面积。(计算结果精确到0.1)
(参考数值:π≈3.14, 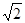 ≈1.41,
≈1.41,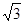 ≈1.73)
≈1.73)
推荐套卷
如图,在△ABC中,以AB为直径的⊙O交AC于点D,直径AB左侧的半圆上有一点动点E(不与点A、B重合),连结EB、ED。
(1)如果∠CBD=∠E,求证:BC是⊙O的切线;
(2)当点E运动到什么位置时,△EDB≌△ABD,并给予证明;
(3)若tanE=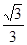 ,BC=
,BC=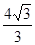 ,求阴影部分的面积。(计算结果精确到0.1)
,求阴影部分的面积。(计算结果精确到0.1)
(参考数值:π≈3.14, 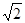 ≈1.41,
≈1.41,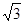 ≈1.73)
≈1.73)