如图①，AB是半圆O的直径，以OA为直径作半圆C，P是半圆C上的一个动点（P与点A，O不重合），AP的延长线交半圆O于点D，其中OA=4．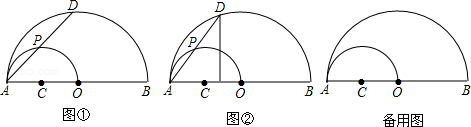
（1）判断线段AP与PD的大小关系，并说明理由；
（2）连接OD，当OD与半圆C相切时，求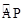
的长；
（3）过点D作DE⊥AB，垂足为E（如图②），设AP=x，OE=y，求y与x之间的函数关系式，并写出x的取值范围．
，
，求
－xy＋
的值
x
⑵
⑷（
π＋1）0－
＋
－
DE⊥AB于E，DF⊥AC于点F，且BE=CF，求证AD⊥BC。
D的高，求证:AD垂直平分EF。(5分)
相关知识点
推荐套卷
如图①，AB是半圆O的直径，以OA为直径作半圆C，P是半圆C上的一个动点（P与点A，O不重合），AP的延长线交半圆O于点D，其中OA=4．
（1）判断线段AP与PD的大小关系，并说明理由；
（2）连接OD，当OD与半圆C相切时，求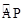的长；
（3）过点D作DE⊥AB，垂足为E（如图②），设AP=x，OE=y，求y与x之间的函数关系式，并写出x的取值范围．
粤公网安备 44130202000953号