如图,将小旗ACDB放于平面直角坐标系中,得到各顶点的坐标为A(﹣6,12),B(﹣6,0),C(0,6),D(﹣6,6).以点B为旋转中心,在平面直角坐标系内将小旗顺时针旋转90°.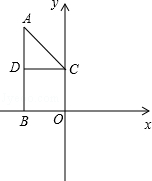
(1)画出旋转后的小旗A′C′D′B′;
(2)写出点A′,C′,D′的坐标;
(3)求出线段BA旋转到B′A′时所扫过的扇形的面积.
相关知识点
推荐套卷
如图,将小旗ACDB放于平面直角坐标系中,得到各顶点的坐标为A(﹣6,12),B(﹣6,0),C(0,6),D(﹣6,6).以点B为旋转中心,在平面直角坐标系内将小旗顺时针旋转90°.
(1)画出旋转后的小旗A′C′D′B′;
(2)写出点A′,C′,D′的坐标;
(3)求出线段BA旋转到B′A′时所扫过的扇形的面积.