2013年6月,某中学结合广西中小学阅读素养评估活动,以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:
(1)在这次抽样调查中,一共调查了多少名学生?
(2)请把折线统计图(图1)补充完整;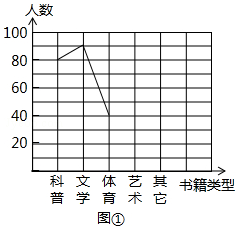
(3)求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;
(4)如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数.
相关知识点
推荐套卷
 抛物线
抛物线 :
: .点F(1,1).
.点F(1,1). (Ⅰ) 求抛物线
(Ⅰ) 求抛物线
 ))(
))( ).连接PF.并延长交抛物线
).连接PF.并延长交抛物线 ),试判断
),试判断 是否成立?请说明理由;
是否成立?请说明理由; :
: ,若
,若 时.
时.


 本题的解答.也可以选用其他方法,按照解答题的一班要求进行解答即可.
本题的解答.也可以选用其他方法,按照解答题的一班要求进行解答即可. ?设每件商品降价x元.每天的销售额为y元.
?设每件商品降价x元.每天的销售额为y元.
 取l.73.结果保留整数).
取l.73.结果保留整数).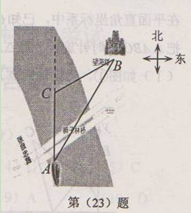
 的值.
的值.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号