如图，在边长为1的正方形组成的网格中，△ABC的顶点均在格点上，点A、B、C的坐标分别是A（﹣2，3）、B（﹣1，2）、C（﹣3，1），△ABC绕点O顺时针旋转90°后得到△A1B1C1．
（1）在正方形网格中作出△A1B1C1；
（2）在旋转过程中，点A经过的路径
的长度为 ；（结果保留π）
（3）在y轴上找一点D，使DB+DB1的值最小，并求出D点坐标．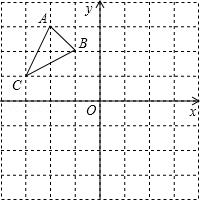
相关试题
的面积． 
关于
轴的对称图形
．
的坐标．
+
—
（2）求x的值：
相关知识点
推荐套卷
如图，在边长为1的正方形组成的网格中，△ABC的顶点均在格点上，点A、B、C的坐标分别是A（﹣2，3）、B（﹣1，2）、C（﹣3，1），△ABC绕点O顺时针旋转90°后得到△A1B1C1．
（1）在正方形网格中作出△A1B1C1；
（2）在旋转过程中，点A经过的路径的长度为 ；（结果保留π）
（3）在y轴上找一点D，使DB+DB1的值最小，并求出D点坐标．
粤公网安备 44130202000953号