已知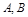 分别是椭圆
分别是椭圆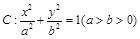 的左、右顶点,点
的左、右顶点,点 在椭圆
在椭圆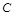 上,且直线
上,且直线 与直线
与直线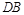 的斜率之积为
的斜率之积为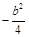 .
.
(Ⅰ)求椭圆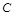 的方程;
的方程;
(Ⅱ)如图,已知 是椭圆
是椭圆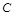 上不同于顶点的两点,直线
上不同于顶点的两点,直线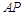 与
与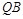 交于点
交于点 ,直线
,直线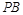 与
与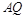 交于点
交于点 .① 求证:
.① 求证: ;② 若弦
;② 若弦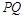 过椭圆的右焦点
过椭圆的右焦点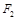 ,求直线
,求直线 的方程.
的方程.
推荐套卷
已知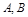 分别是椭圆
分别是椭圆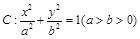 的左、右顶点,点
的左、右顶点,点 在椭圆
在椭圆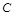 上,且直线
上,且直线 与直线
与直线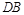 的斜率之积为
的斜率之积为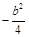 .
.
(Ⅰ)求椭圆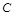 的方程;
的方程;
(Ⅱ)如图,已知 是椭圆
是椭圆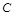 上不同于顶点的两点,直线
上不同于顶点的两点,直线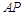 与
与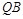 交于点
交于点 ,直线
,直线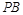 与
与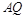 交于点
交于点 .① 求证:
.① 求证: ;② 若弦
;② 若弦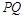 过椭圆的右焦点
过椭圆的右焦点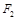 ,求直线
,求直线 的方程.
的方程.