已知直角梯形 中,
中, 是边长为2的等边三角形,
是边长为2的等边三角形,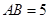 .沿
.沿 将
将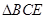 折起,使
折起,使 至
至 处,且
处,且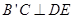 ;然后再将
;然后再将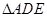 沿
沿 折起,使
折起,使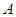 至
至 处,且面
处,且面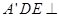 面
面 ,
,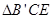 和
和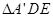 在面
在面 的同侧.
的同侧.

(Ⅰ) 求证: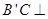 平面
平面 ;
;
(Ⅱ) 求平面 与平面
与平面 所构成的锐二面角的余弦值.
所构成的锐二面角的余弦值.
推荐套卷
已知直角梯形 中,
中, 是边长为2的等边三角形,
是边长为2的等边三角形,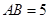 .沿
.沿 将
将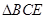 折起,使
折起,使 至
至 处,且
处,且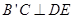 ;然后再将
;然后再将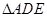 沿
沿 折起,使
折起,使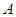 至
至 处,且面
处,且面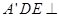 面
面 ,
,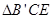 和
和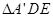 在面
在面 的同侧.
的同侧.

(Ⅰ) 求证: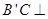 平面
平面 ;
;
(Ⅱ) 求平面 与平面
与平面 所构成的锐二面角的余弦值.
所构成的锐二面角的余弦值.