“五•一”假期,某火车客运站旅客流量不断增大,旅客往往需要长时间排队等候检票.经调查发现,在车站开始检票时,有640人排队检票.检票开始后,仍有旅客继续前来排队检票进站.设旅客按固定的速度增加,检票口检票的速度也是固定的.检票时,每分钟候车室新增排队检票进站16人,每分钟每个检票口检票14人.已知检票的前a分钟只开放了两个检票口.某一天候车室排队等候检票的人数y(人)与检票时间x(分钟)的关系如图所示.
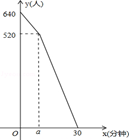
(1)求a的值.
(2)求检票到第20分钟时,候车室排队等候检票的旅客人数.
(3)若要在开始检票后15分钟内让所有排队的旅客都能检票进站,以便后来到站的旅客随到随检,问检票一开始至少需要同时开放几个检票口?