在四边形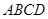 中,对角线
中,对角线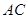 平分
平分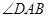 .
.
(1)如图①,当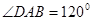 ,
,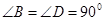 时,求证:
时,求证: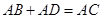 ;
;
(2)如图②,当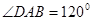 ,
,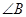 与
与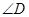 互补时,线段
互补时,线段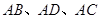 有怎样的数量关系?写出你的猜想,并给予证明;
有怎样的数量关系?写出你的猜想,并给予证明;
(3)如图③,当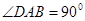 ,
,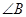 与
与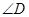 互补时,线段
互补时,线段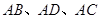 有怎样的数量关系?直接写出你的猜想.
有怎样的数量关系?直接写出你的猜想.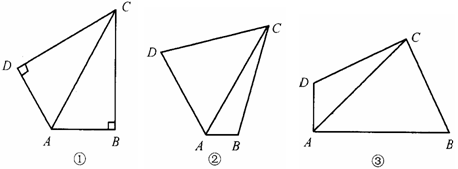
推荐套卷
在四边形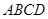 中,对角线
中,对角线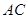 平分
平分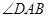 .
.
(1)如图①,当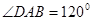 ,
,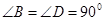 时,求证:
时,求证: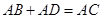 ;
;
(2)如图②,当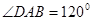 ,
,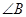 与
与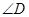 互补时,线段
互补时,线段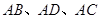 有怎样的数量关系?写出你的猜想,并给予证明;
有怎样的数量关系?写出你的猜想,并给予证明;
(3)如图③,当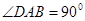 ,
,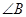 与
与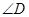 互补时,线段
互补时,线段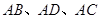 有怎样的数量关系?直接写出你的猜想.
有怎样的数量关系?直接写出你的猜想.