如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(8,0)、(0,6).动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤5).以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为点C、D,连结CD、QC.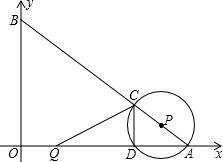
(1)求当t为何值时,点Q与点D重合?
(2)设△QCD的面积为S,试求S与t之间的函数关系,并求S的最大值?
(3)若⊙P与线段QC只有一个交点,请直接写出t的取值范围.
相关知识点
推荐套卷
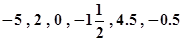 ,
, ,-(-1),并将它们的相反数用“<”符号连接起来.
,-(-1),并将它们的相反数用“<”符号连接起来. )-[(-4
)-[(-4 )]+ |-8+3|
)]+ |-8+3|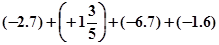
 粤公网安备 44130202000953号
粤公网安备 44130202000953号