在平面直角坐标系xOy中,抛物线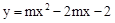 (
( )与y轴交于点A,其对称轴与x轴交于点B。
)与y轴交于点A,其对称轴与x轴交于点B。
(1)求点A,B的坐标;
(2)设直线l与直线AB关于该抛物线的对称轴对称,求直线l的解析式;
(3)若该抛物线在 这一段位于直线l的上方,并且在
这一段位于直线l的上方,并且在 这一段位于直线AB的下方,求该抛物线的解析式。
这一段位于直线AB的下方,求该抛物线的解析式。
相关知识点
推荐套卷
在平面直角坐标系xOy中,抛物线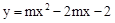 (
( )与y轴交于点A,其对称轴与x轴交于点B。
)与y轴交于点A,其对称轴与x轴交于点B。
(1)求点A,B的坐标;
(2)设直线l与直线AB关于该抛物线的对称轴对称,求直线l的解析式;
(3)若该抛物线在 这一段位于直线l的上方,并且在
这一段位于直线l的上方,并且在 这一段位于直线AB的下方,求该抛物线的解析式。
这一段位于直线AB的下方,求该抛物线的解析式。