某市芙蓉社区为了解家庭月均用水量（单位：吨），从社区中随机抽查100户，获得每户2013年3月的用水量，并制作了频率分布表和频率分布直方图（如图）.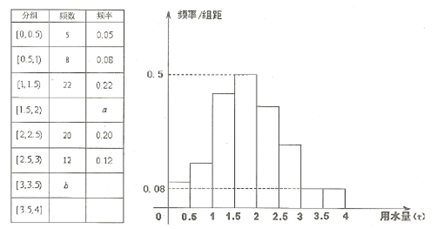
(Ⅰ)分别求出频率分布表中a、b的值，并估计社区内家庭月用水量不超过3吨的频率；
(Ⅱ）设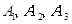
是月用水量为[0，2)的家庭代表.
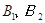是月用水量为[2，4]的家庭代表.若从这五位代表中任选两人参加水价听证会，请列举出所有不同的选法，并求家庭代表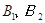至少有一人被选中的概率.
相关试题
，求
的最大值；
，求
的最小值；
，求
的最大值.
}是公比为
的等比数列，
，
，求{
}的前
项和
.
的前
项和为
，且
，
及
；（2）证明：数列
.
为等差数列，
为数列
项和，已知
，求数列
是抛物线
上两动点，直线
分别是抛物线
在点
，
.
1）求点
的纵坐标；
是否经过一定点
的面积的最小值推荐套卷
某市芙蓉社区为了解家庭月均用水量（单位：吨），从社区中随机抽查100户，获得每户2013年3月的用水量，并制作了频率分布表和频率分布直方图（如图）.
(Ⅰ)分别求出频率分布表中a、b的值，并估计社区内家庭月用水量不超过3吨的频率；
(Ⅱ）设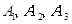是月用水量为[0，2)的家庭代表.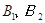是月用水量为[2，4]的家庭代表.若从这五位代表中任选两人参加水价听证会，请列举出所有不同的选法，并求家庭代表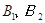至少有一人被选中的概率.
粤公网安备 44130202000953号