如图,抛物线 点 在抛物线 上,过 作 的切线,切点为 ( 为原点 时, 重合于 ),当 时,切线 的斜率为 .
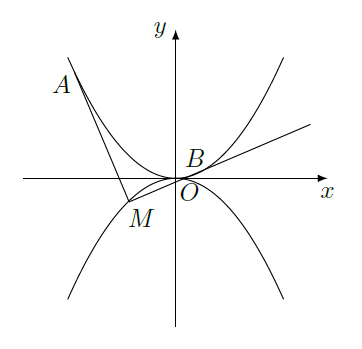
(I)求
的值;
(II)当
在
上运动时,求线段
中点
的轨迹方程(
重合于
时,中点为
).
推荐套卷
如图,抛物线 点 在抛物线 上,过 作 的切线,切点为 ( 为原点 时, 重合于 ),当 时,切线 的斜率为 .

(I)求
的值;
(II)当
在
上运动时,求线段
中点
的轨迹方程(
重合于
时,中点为
).