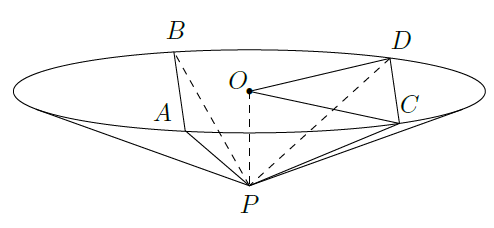
如图，圆锥顶点为
.底面圆心为
，其母线与底面所成的角为
.
和
是底面圆
上的两条平行的弦，轴
与平面
所成的角为
，
（Ⅰ）证明：平面
与平面
的交线平行于底面；
（Ⅱ）求
.
相关试题
其中
为参数．
，讨论函数
的单调性；
与
轴正半轴有交点且交点为
，曲线在点
，求证：对于任意的正实数
．
，首项
，前
项和为
，且
，
，
成等差数列．
的前
．
中
平面
，点
在棱
上，且
，底面为直角梯形，
分别是
的中点．
// 平面
；
与底面
的三内角
的对边分别为 
．
，
，若
的大小．
，
，且△
，求角
的取值范围．
．
，求实数
的取值范围；
的最大值．推荐套卷
如图，圆锥顶点为
.底面圆心为
，其母线与底面所成的角为
.
和
是底面圆
上的两条平行的弦，轴
与平面
所成的角为
，
（Ⅰ）证明：平面
与平面
的交线平行于底面；
（Ⅱ）求
.
粤公网安备 44130202000953号