如图所示，图中的小方格都是边长为1的正方形，△ABC与△A′B′C′是以 点O为位似中心的位似图形，它们的顶点都在小正方形的顶点上.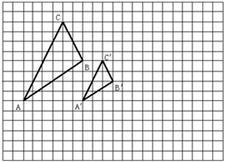 
（1）画出位似中心点O；
（2）直接写出△ABC与△A’B’C’的位似比 ；
（3）以位似中心O为坐标原点，以格线所在直线为坐标轴建立平面直角坐标系，画出△A′B′C′关于点 O中心对称的△A"B"C"，如果△ABC内部一点M的坐标为（x，y），写出△A"B"C"中M的对应点M"的坐标 。
相关试题
，
，
．请选择你最喜欢的两个多项式进行加法运算，并把结果因式分解．
沿数轴向右直爬2个单位到达点
，点
，设点
的值；
的值．
如图，在平面直角坐标系xOy中，抛物线
与x轴交于A（1，0）、
B（5，0）两点．
(1). 【系统题型：作答题】【阅卷方式：手动】求抛物线的解析式和顶点C的坐标；
(2). 【系统题型：作答题】【阅卷方式：手动】设抛物线的对称轴与x轴交于点D，将∠DCB绕点C按顺时针方向旋转，角的两边CD和CB与x轴分别交于点P、Q，设旋转角为
（0°＜＜90°)
①当等于多少度时，△CPQ是等腰三角形？
②设
，求s与t之间的函数关系式．
；
建设新农村，农村大变样.向阳村建起了天然气供应站，气站根据实际情况，每天从零点开始至凌晨4点，只打开进气阀，在以后的16小时(4∶00-20∶00)，同时打开进气阀和供气阀，20∶00-24∶00只打开供气阀，已知气站每小时进气量和供气量是一定的，下图反映了某天储气量
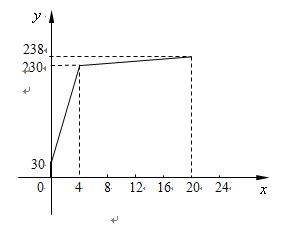
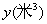与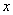
(小时)之间的关系.
(1). 【系统题型：作答题】【阅卷方式：手动】求0∶00-20∶00之间气站每小时增加的储气量；
(2). 【系统题型：作答题】【阅卷方式：手动】求20∶00-24∶00时，
与的函数关系式，并画出函数图象；
相关知识点
推荐套卷
粤公网安备 44130202000953号