已知椭圆C的中心在原点，焦点在x轴上，离心率为
，短轴长为4
.
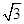(I)求椭圆C的标准方程；
(II)直线x=2与椭圆C交于P、Q两点,A、B是椭圆O上位于直线PQ两侧的动点，且直线AB的斜率为.
①求四边形APBQ面积的最大值；
②设直线PA的斜率为
，直线PB的斜率为
，判断+的值是否为常数，并说明理由．
是一个离散型随机变量，其分布列如下表：求
值，并求
．
在区间
上是减函数．
在
处是否可导．
在
处的连续性与可导性．推荐套卷
已知椭圆C的中心在原点，焦点在x轴上，离心率为，短轴长为4.
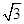(I)求椭圆C的标准方程；
(II)直线x=2与椭圆C交于P、Q两点,A、B是椭圆O上位于直线PQ两侧的动点，且直线AB的斜率为.
①求四边形APBQ面积的最大值；
②设直线PA的斜率为，直线PB的斜率为，判断+的值是否为常数，并说明理由．
粤公网安备 44130202000953号