如图1，
的直径AB=4，点C、D为上两点，且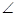
CAB=45°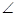，DAB=60°，F为弧BC的中点．沿直径AB折起，使两个半圆所在平面互相垂直，如图2.
(I)求证：OF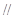
平面ACD；
(Ⅱ)求二面角C—AD—B的余弦值；
(Ⅲ)在弧BD上是否存在点G，使得FG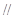平面ACD?若存在，试指出点G的位置；若不存在，请说明理由．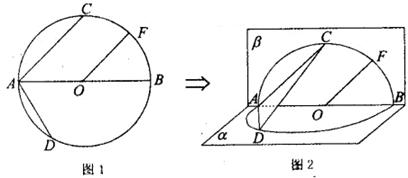
相关试题
，
,
,
,
,
,(
)0,(-2)3,
.推荐套卷
如图1，的直径AB=4，点C、D为上两点，且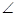CAB=45°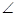，DAB=60°，F为弧BC的中点．沿直径AB折起，使两个半圆所在平面互相垂直，如图2.
(I)求证：OF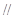平面ACD；
(Ⅱ)求二面角C—AD—B的余弦值；
(Ⅲ)在弧BD上是否存在点G，使得FG平面ACD?若存在，试指出点G的位置；若不存在，请说明理由．
粤公网安备 44130202000953号