某市直小学为了加强管理，对全校教职工实行新的临时事假制度：“每位教职工每月在正常的工作时间，临时有事，可请假至多三次，每次至多一小时”.现对该制度实施以来50名教职工请假的次数进行调查统计，结果如下表所示：
| 请假次数 |
 |
 |
 |
 |
| 人数 |
 |
 |
 |
 |
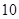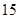根据上表信息解答以下问题：
(1)从该小学任选两名教职工，用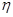
表示这两人请假次数之和，记“函数
在区间
上有且只有一个零点”为事件
，求事件发生的概率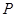
；
(2)从该小学任选两名职工，用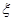
表示这两人请假次数之差的绝对值，求随机变量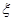的分布列及数学期望
.
相关试题
的底面是边长为1的正方形，
平面
，
，
，求：
中，
平面ABC，D、E分别是BC和
的中点，已知AB=AC=AA1=4，ÐBAC=90°．
⊥平面
；
的余弦值；
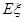的体积．推荐套卷
粤公网安备 44130202000953号