几何体EFG —ABCD的面ABCD，ADGE，DCFG均为矩形，AD=DC=l，AE=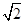
。
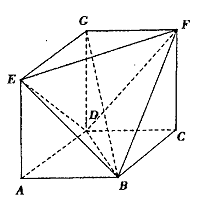
（I）求证：EF⊥平面GDB；
（Ⅱ）线段DG上是否存在点M使直线BM与平面BEF所成的角为45°，若存在求等￥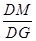
的值；若不存在，说明理由．
相关试题
满足： 
； 
时，求
与
的关系式，并求数列
的模均为1，它们相互之间的夹角均为
。
；
，求
的取值范围。
，函数
，
时，
,求常数
，
的值.
是奇函数. 
的值；
在区间
上单调递增，求实数
的取值范围.
：关于
的不等式
，对一切
恒成立，命题
：函数
是增函数，若
为真，
为假，求实数
的取值范围.推荐套卷
几何体EFG —ABCD的面ABCD，ADGE，DCFG均为矩形，AD=DC=l，AE=。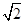
（I）求证：EF⊥平面GDB；
（Ⅱ）线段DG上是否存在点M使直线BM与平面BEF所成的角为45°，若存在求等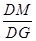￥ 的值；若不存在，说明理由．
粤公网安备 44130202000953号