如图，一次函数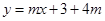（m＜0）的图象经过定点A，与x轴交于点B，与

更新 2022-09-03
科目数学
题型解答题
难度中等
浏览 1725

如图，一次函数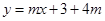（m＜0）的图象经过定点A，与x轴交于点B，与y轴交于点E，AD⊥y轴于点D，将射线AB沿直线AD翻折，交y轴于点C．

（1）用含m的代数式分别表示点B，点E的坐标；
（2）若△ABC中AC边上的高为5，求m的值；
（3）若点P为线段AC中点，是否存在m的值，使△APD与△ABD相似？若存在，请求出m的值；若不存在，请说明理由．

登录免费查看答案和解析

相关试题

如图，已知 $ΔABC$ 内接于 $⊙ O$ ，点 $C$ 在劣弧 $AB$ 上（不与点 $A$ ， $B$ 重合），点 $D$ 为弦 $BC$ 的中点， $DE ⊥ BC$ ， $DE$ 与 $AC$ 的延长线交于点 $E$ ，射线 $AO$ 与射线 $EB$ 交于点 $F$ ，与 $⊙ O$ 交于点 $G$ ，设 $∠ GAB = α$ ， $∠ ACB = β$ ， $∠ EAG + ∠ EBA = γ$ ，

（1）点点同学通过画图和测量得到以下近似数据：

$α$	$30 °$	$40 °$	$50 °$	$60 °$
$β$	$120 °$	$130 °$	$140 °$	$150 °$
$γ$	$150 °$	$140 °$	$130 °$	$120 °$

猜想： $β$ 关于 $α$ 的函数表达式， $γ$ 关于 $α$ 的函数表达式，并给出证明；

（2）若 $γ = 135 °$ ， $CD = 3$ ， $ΔABE$ 的面积为 $ΔABC$ 的面积的4倍，求 $⊙ O$ 半径的长．

题型：未知
难度：未知

收藏答案/解析

在平面直角坐标系中，设二次函数 $y_{1} = (x + a) (x - a - 1)$ ，其中 $a \neq 0$ ．

（1）若函数 $y_{1}$ 的图象经过点 $(1, - 2)$ ，求函数 $y_{1}$ 的表达式；

（2）若一次函数 $y_{2} = ax + b$ 的图象与 $y_{1}$ 的图象经过 $x$ 轴上同一点，探究实数 $a$ ， $b$ 满足的关系式；

（3）已知点 $P (x_{0}$ ， $m)$ 和 $Q (1, n)$ 在函数 $y_{1}$ 的图象上，若 $m < n$ ，求 $x_{0}$ 的取值范围．

题型：未知
难度：未知

收藏答案/解析

如图，在正方形 $ABCD$ 中，点 $G$ 在对角线 $BD$ 上（不与点 $B$ ， $D$ 重合）， $GE ⊥ DC$ 于点 $E$ ， $GF ⊥ BC$ 于点 $F$ ，连接 $AG$ ．

（1）写出线段 $AG$ ， $GE$ ， $GF$ 长度之间的数量关系，并说明理由；

（2）若正方形 $ABCD$ 的边长为1， $∠ AGF = 105 °$ ，求线段 $BG$ 的长．

题型：未知
难度：未知

收藏答案/解析

在面积都相等的所有矩形中，当其中一个矩形的一边长为1时，它的另一边长为3．

（1）设矩形的相邻两边长分别为 $x$ ， $y$ ．

①求 $y$ 关于 $x$ 的函数表达式；

②当 $y ⩾ 3$ 时，求 $x$ 的取值范围；

（2）圆圆说其中有一个矩形的周长为6，方方说有一个矩形的周长为10，你认为圆圆和方方的说法对吗？为什么？

题型：未知
难度：未知

收藏答案/解析

如图，在锐角三角形 $ABC$ 中，点 $D$ ， $E$ 分别在边 $AC$ ， $AB$ 上， $AG ⊥ BC$ 于点 $G$ ， $AF ⊥ DE$ 于点 $F$ ， $∠ EAF = ∠ GAC$ ．

（1）求证： $ΔADE ∽ ΔABC$ ；

（2）若 $AD = 3$ ， $AB = 5$ ，求 $\frac{AF}{AG}$ 的值．

题型：未知
难度：未知

收藏答案/解析

推荐套卷

热门套卷