椭圆
的离心率为
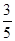，两焦点分别为
，点M是椭圆C上一点，
的周长为16，设线段MO（O为坐标原点）与圆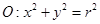
交于点N，且线段MN长度的最小值为
.
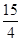（1）求椭圆C以及圆O的方程；
（2）当点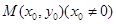
在椭圆C上运动时，判断直线
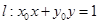与圆O的位置关系.
相关试题
对于满足
的一切m的值都成立,求x的取值范围.
,直线
过点P(
)
与直线
交于A,B两点(易于原点O),且以AB为直径的圆恰好过原点.
面积的最小值.
与椭圆
恒有公共点，求实数
的取值范围推荐套卷
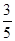椭圆的离心率为，两焦点分别为，点M是椭圆C上一点，的周长为16，设线段MO（O为坐标原点）与圆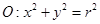交于点N，且线段MN长度的最小值为.
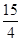（1）求椭圆C以及圆O的方程；
（2）当点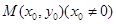在椭圆C上运动时，判断直线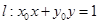与圆O的位置关系.
粤公网安备 44130202000953号