椭圆 :
: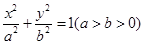 的右焦点为
的右焦点为 且
且 为常数,离心率为
为常数,离心率为 ,过焦点
,过焦点 、倾斜角为
、倾斜角为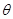 的直线
的直线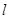 交椭圆
交椭圆 与M,N两点,
与M,N两点,
(1)求椭圆 的标准方程;
的标准方程;
(2)当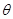 =
= 时,
时, =
= ,求实数
,求实数 的值;
的值;
(3)试问 的值是否与直线
的值是否与直线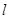 的倾斜角
的倾斜角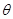 的大小无关,并证明你的结论
的大小无关,并证明你的结论
推荐套卷
椭圆 :
: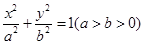 的右焦点为
的右焦点为 且
且 为常数,离心率为
为常数,离心率为 ,过焦点
,过焦点 、倾斜角为
、倾斜角为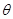 的直线
的直线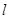 交椭圆
交椭圆 与M,N两点,
与M,N两点,
(1)求椭圆 的标准方程;
的标准方程;
(2)当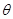 =
= 时,
时, =
= ,求实数
,求实数 的值;
的值;
(3)试问 的值是否与直线
的值是否与直线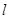 的倾斜角
的倾斜角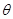 的大小无关,并证明你的结论
的大小无关,并证明你的结论