如图，在四棱锥P－ABCD中，底面是边长为2
的菱形，且∠BAD＝120°，且PA⊥平面ABCD，PA＝
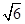，M，N分别为PB，PD的中点．
(1)证明：MN∥平面ABCD；
(2) 过点A作AQ⊥PC，垂足为点Q，求二面角A－MN－Q的平面角的余弦值．
相关试题
中，角
的对边分别为
，且满足
.
的大小；（2）设
，
，求
的最小值.
为实数，函数
的单调区间
且
时，有
恰有一个零点，求实数
满足
并猜想
的表达式
，若函数
在
上有3个零点，求实数
的取值范围.
推荐套卷
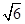如图，在四棱锥P－ABCD中，底面是边长为2的菱形，且∠BAD＝120°，且PA⊥平面ABCD，PA＝，M，N分别为PB，PD的中点．
(1)证明：MN∥平面ABCD；
(2) 过点A作AQ⊥PC，垂足为点Q，求二面角A－MN－Q的平面角的余弦值．
粤公网安备 44130202000953号