已知：A(a，y1)、B(2a，y2)是反比例函数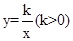
图像上的两点．
(1)比较y1与y2的大小关系；
(2)若A、B两点在一次函数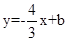
第一象限的图像上(如图所示)，分别过A、B两点作x轴的垂线，垂足分别为C、D，连结OA、OB，且S△OAB=8，求a的值；
(3)在(2)的条件下，如果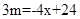
，
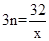，求使得m>n的x的取值范围．
，其中
.
－2x－3=0．相关知识点
推荐套卷
已知：A(a，y1)、B(2a，y2)是反比例函数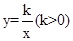图像上的两点．
(1)比较y1与y2的大小关系；
(2)若A、B两点在一次函数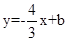 第一象限的图像上(如图所示)，分别过A、B两点作x轴的垂线，垂足分别为C、D，连结OA、OB，且S△OAB=8，求a的值；
(3)在(2)的条件下，如果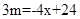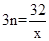，，求使得m>n的x的取值范围．
粤公网安备 44130202000953号