在平面直角坐标系xOy中,抛物线 经过原点O, 点B(-2,n)在这条抛物线上.
经过原点O, 点B(-2,n)在这条抛物线上.

(1)求抛物线的解析式;
(2)将直线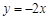 沿y轴向下平移b个单位后得到直线l, 若直线l经过B点,求n、b的值;
沿y轴向下平移b个单位后得到直线l, 若直线l经过B点,求n、b的值;
(3)在(2)的条件下,设抛物线的对称轴与x轴交于点C,直线l与y轴交于点D,且与抛物线的对称轴交于点E.若P是抛物线上一点,且PB=PE,求P点的坐标.
在平面直角坐标系xOy中,抛物线 经过原点O, 点B(-2,n)在这条抛物线上.
经过原点O, 点B(-2,n)在这条抛物线上.

(1)求抛物线的解析式;
(2)将直线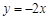 沿y轴向下平移b个单位后得到直线l, 若直线l经过B点,求n、b的值;
沿y轴向下平移b个单位后得到直线l, 若直线l经过B点,求n、b的值;
(3)在(2)的条件下,设抛物线的对称轴与x轴交于点C,直线l与y轴交于点D,且与抛物线的对称轴交于点E.若P是抛物线上一点,且PB=PE,求P点的坐标.