某工厂生产一种仪器的元件,由于受生产能力和技术水平的限制,会产生一些次品,根据经验知道,其次品率P与日产量x(万件)之间大体满足关系: (其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(1)试将生产这种仪器的元件每天的盈利额T(万元)表示为日产量x(万件)的函数;
(2)当日产量为多少时,可获得最大利润?
相关知识点
推荐套卷
 为何值时,复数
为何值时,复数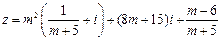 .
. 对应的点落在射线
对应的点落在射线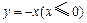 上,
上, ,求复数
,求复数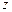 .
.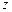 是虚数
是虚数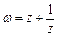 是实数,且
是实数,且 .
.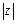 的值及
的值及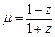 ,求证:
,求证: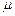 为纯虚数;
为纯虚数;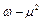 的最小值.
的最小值.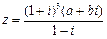 且
且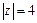 ,
,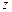 对应的点在第一象限内,若复数
对应的点在第一象限内,若复数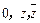 对应的点是正三角形的三个顶点,求实数
对应的点是正三角形的三个顶点,求实数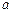 ,
,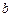 的值.
的值. ,当实数
,当实数 为何值时,
为何值时, 为实数;
为实数; 粤公网安备 44130202000953号
粤公网安备 44130202000953号