三月份学校团委组织开展了“学雷锋”系列活动.活动结束后,为了表彰优秀,团委王老师准备用一笔钱购买奖品.如果以1支钢笔和2本笔记本为一份奖品,则可买60份奖品;如果以1支钢笔和3本笔记本为一份奖品,则可以买50份奖品.
(1)如果这笔钱刚好有600元,试求出每支钢笔和每本笔记本的价格多少?
(2)如果用这笔钱全部购买钢笔,问:总共可以买几支?
(3)如果王老师用这笔钱恰好能买30份同样的奖品,那么可以选择几支钢笔和几本笔记本作为一份奖品?请你写出所有可能的情况供王老师选择.
相关知识点
推荐套卷

 ;(2)
;(2)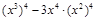 ;(3)
;(3) .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号