如图，菱形ABCD中，对角线AC、BD交于点O，点P在对角线BD上运动（B、D两点除外），线段PA绕点P顺时针旋转m°(0＜m°＜180º） 得线段PQ.
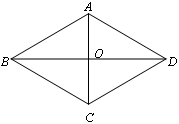
（1）当点Q与点D重合，请在图中用尺规作出点P所处的位置（不写作法，保留作图痕迹）；
（2）若点Q落在边CD上（C点除外），且∠ADB=n°.
①探究m与n之间的数量关系；
②当点P在线段OB上运动时，存在点Q，使PQ=QD，直接写出n的取值范围.
相关试题
中，
⊥
，
，
，
，求
的长和
的值．
，其中
．
的半径为6，线段
与⊙
、
，
，
，
与⊙
，设
，
．
长；
关于
的函数解析式，并写出定义域；
⊥
时，求
的长．
的图像与
轴、
轴分别相交于点
、
．二次函数的图像与
，与这个一次函数的图像相交于点
，
．
，求这个二次函数的解析式．相关知识点
推荐套卷
粤公网安备 44130202000953号